enum cv::NormTypes
Overview
norm types
- For one array:
#include <base.hpp> enum NormTypes { NORM_INF = 1, NORM_L1 = 2, NORM_L2 = 4, NORM_L2SQR = 5, NORM_HAMMING = 6, NORM_HAMMING2 = 7, NORM_TYPE_MASK = 7, NORM_RELATIVE = 8, NORM_MINMAX = 32, };
Detailed Documentation
norm types
For one array:
\[norm = \forkthree{\|\texttt{src1}\|_{L_{\infty}} = \max _I | \texttt{src1} (I)|}{if \(\texttt{normType} = \texttt{NORM_INF}\) } { \| \texttt{src1} \| _{L_1} = \sum _I | \texttt{src1} (I)|}{if \(\texttt{normType} = \texttt{NORM_L1}\) } { \| \texttt{src1} \| _{L_2} = \sqrt{\sum_I \texttt{src1}(I)^2} }{if \(\texttt{normType} = \texttt{NORM_L2}\) }\]Absolute norm for two arrays
\[norm = \forkthree{\|\texttt{src1}-\texttt{src2}\|_{L_{\infty}} = \max _I | \texttt{src1} (I) - \texttt{src2} (I)|}{if \(\texttt{normType} = \texttt{NORM_INF}\) } { \| \texttt{src1} - \texttt{src2} \| _{L_1} = \sum _I | \texttt{src1} (I) - \texttt{src2} (I)|}{if \(\texttt{normType} = \texttt{NORM_L1}\) } { \| \texttt{src1} - \texttt{src2} \| _{L_2} = \sqrt{\sum_I (\texttt{src1}(I) - \texttt{src2}(I))^2} }{if \(\texttt{normType} = \texttt{NORM_L2}\) }\]Relative norm for two arrays
\[norm = \forkthree{\frac{\|\texttt{src1}-\texttt{src2}\|_{L_{\infty}} }{\|\texttt{src2}\|_{L_{\infty}} }}{if \(\texttt{normType} = \texttt{NORM_RELATIVE_INF}\) } { \frac{\|\texttt{src1}-\texttt{src2}\|_{L_1} }{\|\texttt{src2}\|_{L_1}} }{if \(\texttt{normType} = \texttt{NORM_RELATIVE_L1}\) } { \frac{\|\texttt{src1}-\texttt{src2}\|_{L_2} }{\|\texttt{src2}\|_{L_2}} }{if \(\texttt{normType} = \texttt{NORM_RELATIVE_L2}\) }\]
As example for one array consider the function \(r(x)= \begin{pmatrix} x \\ 1-x \end{pmatrix}, x \in [-1;1]\). The \(L_{1}, L_{2}\) and \(L_{\infty}\) norm for the sample value \(r(-1) = \begin{pmatrix} -1 \\ 2 \end{pmatrix}\) is calculated as follows
\[\begin{split}\begin{align*} \| r(-1) \|_{L_1} &= |-1| + |2| = 3 \\ \| r(-1) \|_{L_2} &= \sqrt{(-1)^{2} + (2)^{2}} = \sqrt{5} \\ \| r(-1) \|_{L_\infty} &= \max(|-1|,|2|) = 2 \end{align*}\end{split}\]
and for \(r(0.5) = \begin{pmatrix} 0.5 \\ 0.5 \end{pmatrix}\) the calculation is
\[\begin{split}\begin{align*} \| r(0.5) \|_{L_1} &= |0.5| + |0.5| = 1 \\ \| r(0.5) \|_{L_2} &= \sqrt{(0.5)^{2} + (0.5)^{2}} = \sqrt{0.5} \\ \| r(0.5) \|_{L_\infty} &= \max(|0.5|,|0.5|) = 0.5. \end{align*}\end{split}\]
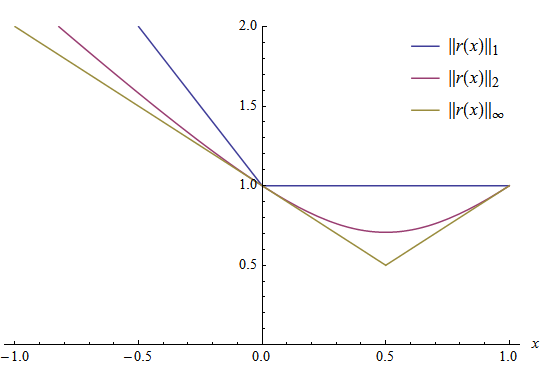
The following graphic shows all values for the three norm functions \(\| r(x) \|_{L_1}, \| r(x) \|_{L_2}\) and \(\| r(x) \|_{L_\infty}\). It is notable that the \(L_{1}\) norm forms the upper and the \(L_{\infty}\) norm forms the lower border for the example function \(r(x)\).
Enum Values
NORM_RELATIVE
flag
NORM_MINMAX
flag